Keyword [Resolution Discrepancy]
Touvron H, Vedaldi A, Douze M, et al. Fixing the train-test resolution discrepancy[J]. arXiv preprint arXiv:1906.06423, 2019.
1. Overview
1.1. Motivation
Existing augmentations induce a significant discrepancy between training (RandomResizedCrop) and testing (CenterCrop after resizing shorter dimension to $K_{test}^{image}$).

In this paper, it proposes simple strategy to optimize performance when train and test resolutions differ.
1) Increase both the size of test image size $K_{test}^{image}$ and test image center crop size $K_{test}$.
2) Define an equalization mapping from the new distribution back to the old one via a scalar transformation, and apply it as an activation function after the pooling layer.
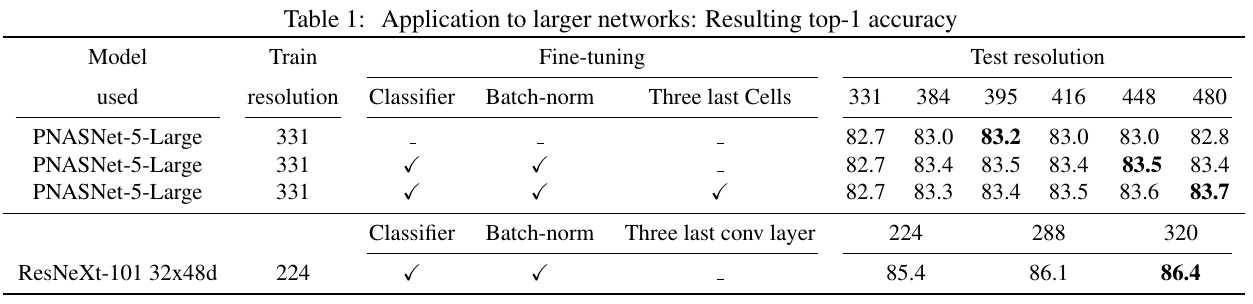
3) Finetune the very last layers of the network (include BN) on the same training set, after switching the crop size $K_{train}$ to $K_{test}$.

1) Better accuracy is obtained with higher resolution crops at test time than at train time.
2. Analysis
1) Resizing operation changes the apparent size of the objects.
2) Different crop size has an effect on the statistics of the network activations, especially after global pooling layers.

3. Methods
1) Difference in apparent object sizes at training and testing time can be removed by increasing the crop size at test time.
2) Adjust the network before the global average pooling to compensate for the change in activation statistics.
3.1. Adjust Crop Size
Increase $K_{test}^{image}$ and crop size $K_{test}$ to keep $K_{test}^{image} / K_{test}$ fixed.

3.2. Adjust Statistics before Spatial Pooling
1) Define an equalization mapping from the new distribution back to the old one via a scalar transformation, and apply it as an activation function after the pooling layer.
$P(x,\mu,\sigma) = e^{-(1 + \frac{\xi}{\sigma}(x-\mu))^{-1/\xi} }$.
- Observed that $\xi$ can be kept constant at 0.3 to fit the distribution.
- Compute $\mu_{ref}, \sigma_{ref}$ observed on training images time for $K_{test} = K_{trian}$.
- Then increase $K_{test}$ to target resolution and measure $\mu_0, \sigma_0$ again.

2) Finetune the very last layers of the network (include BN) on the same training set, after switching the crop size $K_{train}$ to $K_{test}$.

4. Experiments